トライアドコードとグラフ理論 #2

見切れている数式はスクロールすると読めます
今回は前回の記事の続きです.定義などは前回の記事に倣います.
今回からはトライアドコードグラフを同型を除いて分類することを考えます.トライアドコードグラフは構成の定義から高々 個しかありません.なので,全部書いてみて分類するのでもいいですが,やはり数学的に分類を与えてみたいところです.
まず,トライアドコードグラフが非連結である場合を考え,その次に連結な場合を考えます.
非連結なトライアドコードグラフの分類
証明
(if part)
は連結なので,点
と点
の間に道が存在する.この道は
の構成から,
から
をいくつか足し,さらに
をいくつか足すことで到達できるので,それらの回数をそれぞれ
とすれば
を得る.

(only if part)
から
へ,
から
へ,同様に
まで辺で繋がっているので連結である.

注 (2.1)はほとんどの場合において, が互いに素であれば,またそのときに限り
が連結であるということを主張している.しかし
はGCD整域でないため,最大公約数が一意的に定まらない.例えば,
のときは(一般的な意味での)最大公約数は
となり連結でないように思われるが,
においては,
となるので, は連結である.実際
となりsus4グラフと同型であり,これは前回の記事にも書いたように連結グラフである.
sus4グラフのトーラス埋め込み pic.twitter.com/dlODkdaWL5
— だふやふ🍟🍚 (@dafuyafu) 2018年7月9日
注 (2.1)は環論の言葉で言えば, が連結であることと
であることが同値であるとも言える.このとき,
と
の線形結合で任意の
の元を表せる,と言い換えられるので,
が任意の点と辺で繋がっている(道がある),つまり連結である,と簡潔に言及できるので,なんか嬉しい.
注 群論の知識を使うと,(2.1)における の部分は
および
でもよい.これらの数は
を巡回群としてみたときの生成元であることに注意する.
(2.1)の対偶を取ればトライアドコードグラフが非連結であるための必要十分条件を得る.そしてそれは,多少の誤謬を認めて簡単に言えば が
より大きい約数を持つことである.以下ではより正確に記述していく.
定義 グラフ について,その連結成分数を
と表す.また,
の同型による同値類を
と表す.
(略証) 頂点 は
と辺で繋がっている.

このうち,
のいずれかが成り立つときに頂点が重なる事があるが,これらは によらず一定.つまり,重なり方は
のみによって決まるので任意の頂点の次数は等しい.
証明 これらの値を取るグラフは実際に構成できるので,これ以上にならないことを示せば良い.トライアドコードグラフは構成の定義から3次完全グラフ の組み合わせから成るので,任意の頂点の次数は
以上でなければならない.しかし
の場合は少なくとも1つ次数が
以下の点が存在するので矛盾する.
以上より非連結なトライアドコードグラフは連結成分数が および
であることがわかった.連結成分数がそれぞれの値を取るのはどのような場合かを考察する.
証明
(only if part) 書けばわかる.

(if part) 個の頂点からなる正則なグラフにおいて,
つある連結成分の頂点は必ず
つでなければならない.実際,頂点が
つからなる連結成分が存在するとき,その連結成分の頂点の次数は
以下となり矛盾.よってそのグラフは
が4つからなるグラフとなり,それはすなわち
である.
注 は音楽におけるオーグメントコードを表していた.

オーグメントコードは根音,長3度,短6度からなるトライアドコードである.聞いてみればわかるが,若干濁ったコードであり,
VIm → V#aug → I → II
のようにして主に展開系として用いられる.なお, と同型なグラフは自分自身だけであるので,実際は
である.
証明
(only if part) 書けばわかる.

(if part) 3つある連結成分の頂点数は全て4でなければならない.もし,頂点数が3以下の連結成分があるとすると,その連結成分の頂点の次数は2になるが,正則性から他の頂点の次数も2になる.すると,頂点数が5以上の連結成分で頂点の次数が2になると,それは の組み合わせで構成されることと矛盾する.よって条件を満たすグラフは
のみである.
注 は音楽におけるディミニッシュコードを表していた.

ディミニッシュコードは根音,短3度,減5度からなるトライアドコードである.聞いてみればわかるが,これもまた濁ったコードであり,主に Ⅵm への展開前に
V → V#dim → VIm
という具合に使うとかっこいい.このようにして筆者もよく使う.
ちょっと長くなってしまったので今回はこの辺にします.
トライアドコードとグラフ理論 #1
見切れている数式はスクロールで読めます

先日,オムニバス講義のグラフ理論回で,
トライアドコードのグラフをつなげてメービウスの帯を作る
という大変興味深い研究を知りました.
ここでは詳しくは説明しませんが,「n-triad coloring」と検索すれば出てくると思います.
ただ,その講義の中ではドからシまでの白鍵のみを考えていたため,特にメジャーやマイナーといった音階的な分類がされていなかったのが自分的に少し引っかかりました.そこで,黒鍵もすべて含めて同じようにコードからグラフを作ったらどうなるか?と考えたことがきっかけです.
Abstract
この記事では音楽におけるトライアドコードから着想を得たトライアドコードグラフを定義し,トライアドコードグラフのいくつかの同型が存在すること,連結成分数がほとんどすべての場合においてパラメータの最大公約数になることを証明し,それを用いて6つの主要なトライアドコードについてそのグラフの考察を与える.主要な結果としては,メジャートライアドコードグラフとマイナートライアドコードグラフは同型でありトーラス埋め込み可能であること,フラットファイブコードは2つの6次完全グラフを連結成分として持つことなどが分かった.
本論
定義 1 (ただし,
)1 について,
とし, とする.この
を
トライアドコードグラフ という.
例 2.1 最も初等的なトライアドコードはメジャートライアドコードである.以下にそのトライアドコードグラフの構成を記す.以降,メジャートライアドコードグラフを と表す.
今,無限に長いピアノの鍵盤のうち,ドを0,その上のシを11とする同値関係で割ることで鍵盤を で巡回していると考える.

メジャートライアドコードはルート,それに対する長三度と完全五度という3音からなる.例えばルートが「ド」のときは「ミ」と「ソ」である.これを に対応させるとそれぞれ「0」「4」「7」となる.

これは代数的には,ルート に対して
の音からなると考えられるので,トライアドコードグラフは
と表される.
を
から
まで動かすと三角形のグラフが
個できる.

これらの三角形の中で,数が同じである頂点を全てつなげることで が作られる.トーラス上ではこのように表される.

以上のようにして が構成される.
例 2.2 主要なトライアドコードをもう5つ挙げる.
- マイナートライアドコードは
と表される.
- ディミニッシュコードは
と表される.
- オーギュメントコードは
と表される.
- sus4コードは
と表される.
- フラットファイブコードは
と表される.
補題 3 以下のような自明なグラフ同型が存在する.
略証 トライアドコードはベース音のとり方が3通り存在し,それぞれルートを1番目,2番目,3番目に取るようにベース音を取ったコードに対応しており,いずれも同じトライアドコードを表す.


例 4 マイナーコードグラフについて以下の自明な同型が存在する.
注 4.1 自明な同型といった場合には上の3つのみを指す.音楽的には同じコードで3つのベース音のとり方がある(トライアドコードが3つの音からなるコードだから)が,代数的にも上の3つに限られることが分かる.例えば, という同型だけ考えると,
\begin{align*} \gg(m,n) &\simeq \gg(n-m, -m)\\ &\simeq \gg(-m - (n-m), -(n-m)) = \gg(-n, m-n)\\ &\simeq \gg( (m-n)-(-n), -(-n) ) = \gg(m,n) \end{align*}
となり,同型は3つのみであることが分かる.他の自明な同型についても同様である.
証明
における頂点
を一つ固定して考える.頂点
からは以下のように最大で6つの頂点に辺が伸びている.

このうち, と
という2つの頂点に着目する.
Claim: 任意の で以下が成り立つ.
図より,明らかに .よって
を示せば良い.いま,
は
の頂点である.さらにトライアドグラフの定義より,この頂点からは
と
の両方に辺が伸びており,
と
自体も辺で繋がっている事がわかる.よって主張は成り立つ.

主張が成り立つので, となる.同じ方法を
に適応することによって逆向きの包含が示せる.また,頂点の集合は明らかに等しい.よって2つのグラフは同型である.
系 6 である.すなわちメジャーコードグラフとマイナーコードグラフは同型である.
証明
注 このように,違うコードであるにもかかわらずそのコードグラフが同型になる場合がある.ここで,補題3にあるような同型は音楽的に同じコードを表すという意味で自明な同型であるが,集合論的には違うコードを表していることに注意が必要である.人間的には同じ響きかもしれないが,それらは数学的には異質であるということである.
注 この記事の表題にある画像は, と
が同型であることを図で示しているが,数学的にもこれらのグラフが同型であることが (系6) で示される.
スケッチ
以下では味わい深い事柄を少し並べる.
トーラス的トライアドコードグラフ
メジャートライアドコードグラフ ,マイナートライアドコードグラフ
およびsus4コードグラフ
はそれぞれトーラス的である.つまり,トーラス上に埋め込むことができる.
は同型なので上の例のようにトーラスに埋め込まれる.また,
は以下のように埋め込まれる.
sus4グラフのトーラス埋め込み pic.twitter.com/dlODkdaWL5
— だふやふ🍟🍚 (@dafuyafu) 2018年7月9日
メジャートライアドコードの部分スケール
を以下のように表す.

同じ数字の頂点は同じだと思えば,これはトーラス埋め込みだと思える.このグラフは,任意のルートについてそのメジャーペンタトニックスケールを連結部分として持つ.

さらに,沖縄音階についても同様である.

証明は簡単なので読者の演習とする.
今回は以上です.次回はトライアドコードグラフの正則性と連結成分について考えたいと思います.査読よろしくお願い致します.
-
における大小関係を便宜上
とする.↩
Milnor - The Fundamental Theorem of Algebra (Topology from the Differentiable Viewpoint)
見切れている数式はスクロールで読めます.
今日は趣向を変えてミルナー著「Topology from the Differentiable Viewpoint」から代数学の基本定理の証明を紹介します.ちょうど微分トポロジーの授業でここの部分が僕の担当だったからです.
代数学の基本定理は複素数体が代数閉体であるというものですが,なんか沢山証明方法はあるみたいですが,ミルナー本にあるやつを解説したサイトは見かけなかったので,今日はそこを書いてみるなー(激ウマギャグ)
流れ
まず証明の流れから説明すると,
- 一変数複素係数多項式とステレオグラフ射影を用いて単位球面から単位球面への写像を考える.
- その写像が単位球面上滑らかであることを示す.
- さらにその写像が全射であることを,正則点の個数の関数を用いて示す.
- 定理に結びつける.
という感じです.
証明
(証明)
任意の について,
(ただし
) を用いて
と表されているとする. は
から
への関数を定めるが,実部と虚部に分けて考えても2つとも多項式で表されているので,通常の微分に関して滑らかである.
今、3次元実ユークリッド空間 に単位球面
があると考える.

ここで,単位球面の北極 から
平面へのステレオグラフ射影
を考える.
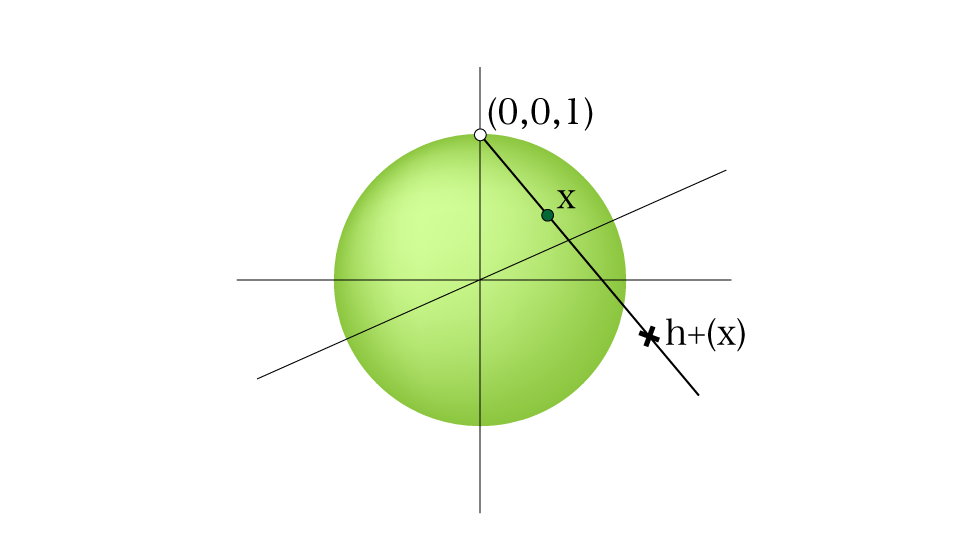
定式的には,
となり,北極以外の の点
を,北極から
に引いた半直線が
平面にぶつかる点に送る滑らかな写像である.
これらを用いて次のような写像 を考える.
\begin{equation} f(x) = \begin{cases} h_+^{-1} \circ P \circ h_+ (x) & (x \neq (0,0,1))\\ (0,0,1) & (x = (0,0,1)) \end{cases} \end{equation}
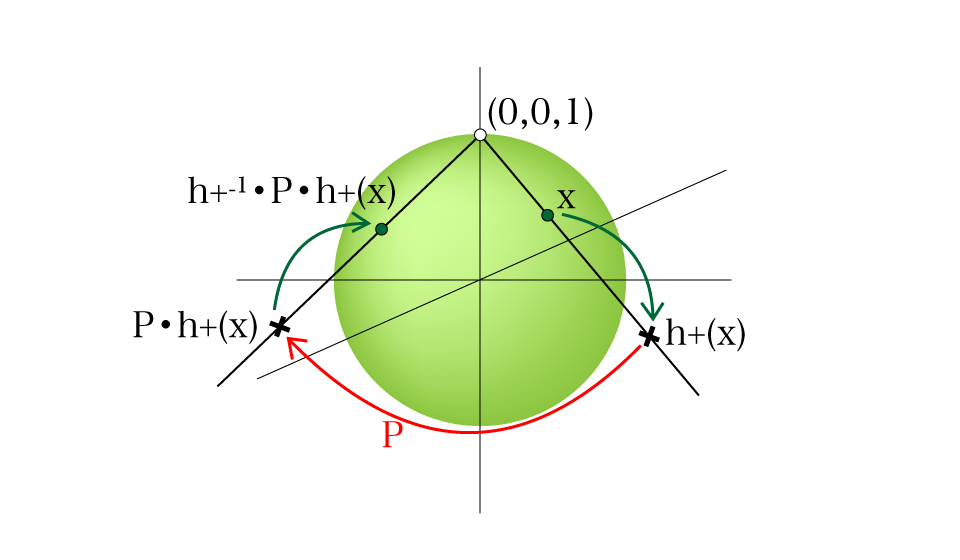
これは,単位球面上の 以外の点を
平面上にステレオグラフ射影し,この平面を複素平面だと思って
で別の複素数に送り,ステレオグラフ射影で単位球面に引き戻すような写像である.
 が
が  上滑らかであること
上滑らかであること
構成より, は
においては滑らかな写像の合成であるので,
もまた滑らかである.これが
の近傍においても,つまり定義域において
が滑らかな写像であることを示す.まず,南極
から
平面へのステレオグラフ射影を
とし,
を
とする.
においては,
であることから,
と表される.ここで, を計算する.

複素数 を含むように空間を縦で割ると上図のように表される.

赤色と青色の三角形は「直角以外の一つの角が等しい」ので相似である.
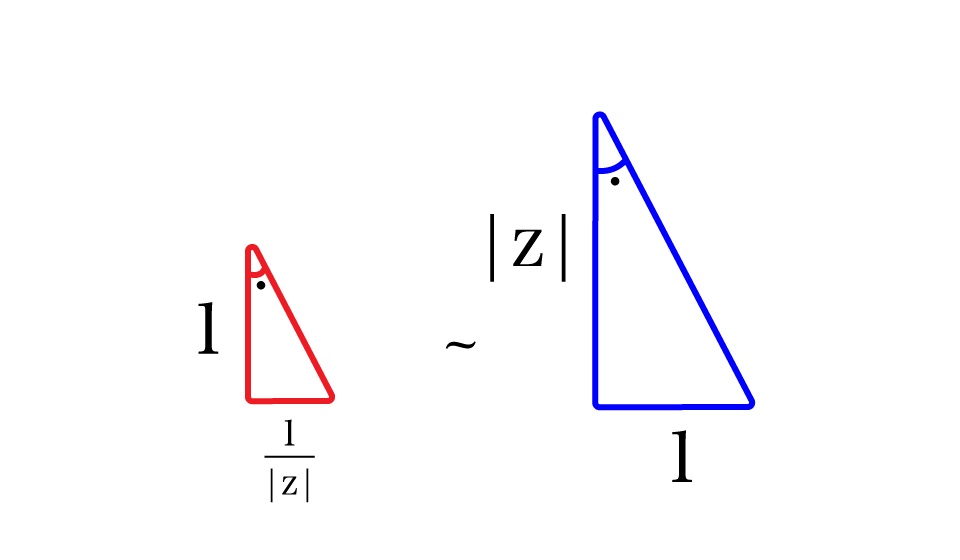
すると,赤色の三角形のうち,ちょうど のノルムに対応する辺の長さは
であることが分かる.よって,求めたい実際の複素数
は,その単位ベクトルにノルムをかけたものであるので,
\begin{equation} h_+ \circ h_-^{-1}(z) = \frac{1}{|z|} \cdot \frac{z}{|z|} = \frac{1}{\overline{z}} \end{equation}
以上のことから, を整理する.複素共役は積や和に分解し,複素共役の複素共役は元の複素数になることなどを用いると,
\begin{align*} Q(z) &= h_- \circ h_+^{-1} \circ P \circ h_+\circ h_-^{-1} (z)\\ &= h_- \circ h_+^{-1} \circ P (1/\overline{z})\\ &= h_- \circ h_+^{-1} (a_0 (1/\overline{z})^n + \cdots + a_{n-1} (1/\overline{z}) + a_n)\\ &= 1 / \overline{(a_0 (1/\overline{z})^n + \cdots + a_{n-1} (1/\overline{z}) + a_n)}\\ &= 1 / (\overline{a_0} \overline{(1/\overline{z})^n} + \cdots + \overline{a_{n-1}} \overline{(1/\overline{z})} + \overline{a_n})\\ &= 1 / (\overline{a_0} (1/z)^n + \cdots + \overline{a_{n-1}} (1/z) + \overline{a_n})\\ &= z^n / (\overline{a_0} + \overline{a_1} z + \cdots + \overline{a_n} z^n) \end{align*}
となる.すると, であることから
は
においても値
をもち,さらに有理関数の形で表されるので滑らかな関数である.よって,
もまた滑らかな関数となる.
 の臨界値が高々有限個であること
の臨界値が高々有限個であること
は複素関数であり,実部と虚部に分けることで実数値関数の対と考えることができる.つまり,実数係数多項式
を用いて
と表すことができる.ここで,
は多項式によって表される関数であるので複素正則関数である.よってコーシー・リーマンの方程式が成り立つ.今の場合,
\begin{equation} \frac{\partial P_1}{\partial x} = \frac{\partial P_2}{\partial y},\quad \frac{\partial P_1}{\partial y} = - \frac{\partial P_2}{\partial x} \end{equation}
となる.また,
\begin{equation} \frac{d P_1}{d x} = \frac{\partial P_1}{\partial x} + \sqrt{-1} \frac{\partial P_2}{\partial x} \end{equation}
となる.
これを複素数だと思うと,そのノルムの二乗は
\begin{equation} \begin{array}{|c|} \frac{d P_1}{d x} \end{array}^2 = \left( \frac{\partial P_1}{\partial x} \right)^2 + \left( \frac{\partial P_2}{\partial x} \right)^2 \end{equation}
となるが,複素関数 のヤコビ行列
は
\begin{equation} J(P) = \left[ \begin{array}{cc} \frac{\partial P_1}{\partial x} & \frac{\partial P_1}{\partial y}\\ \frac{\partial P_2}{\partial x} & \frac{\partial P_2}{\partial y} \end{array} \right] \end{equation}
となることから,ヤコビ行列の行列式は
\begin{equation} \mathrm{det} J(P)= \left( \frac{\partial P_1}{\partial x} \right)^2 + \left( \frac{\partial P_2}{\partial x} \right)^2 \end{equation}
となり,ちょうど
\begin{equation} \begin{array}{|c|} \frac{d P_1}{d x} \end{array}^2 = \mathrm{det} J(P) \end{equation}
となることが分かる.ここで,ヤコビ行列の行列式が になる点が
の臨界点であることから,
の臨界点は
である点に対応することが分かる.しかし,
は定数でない多項式であったので,
もまた多項式であるので,
になる点は有限個しかない.
よって の臨界点は有限個しかないので,構成から
もまた臨界点は有限個しかなく,故に臨界値は有限個に限られる.
連結位相空間上の局所定数関数は定数関数であること
ここで,題にあるような補題を証明する.
を連結空間,
を局所定数関数とする.任意の
の点
を一つ固定して考える.
を
とする.定義から,,
である.
ここで, がそれぞれ
の開集合であることを示す.
任意に を取る.定義より
である.ここで,
は定数関数であることから,ある
を含む開集合
が存在して,任意の
について
となる.
よって,任意の について
となるので
となる.
ここで,任意に取った を
の中で動かすことで,
は
を被覆することが分かる.つまり,
\begin{equation} C_0 = \bigcup_{y_i \in C_0} U_i \end{equation}
となる.各 は開集合なので,その可算個の和集合である
もまた開集合となる.同様にして
も開集合であることが示せる.
以上より は開集合となるが,
は連結空間なので,交わらない開集合で分割することはできないはずである.よって
のいずれかになる.しかし,今 を固定して考えていたが,
自体は
を満たすので,
であることから,
は空集合ではない.よって1つめのパターンとなる.
よって 全体で
は一定の値を取るので,全体でも定数関数となる.
帰結
今, は連結空間である.
の臨界値は有限個であったので,正則値全体は連結である.(
無限連結空間から有限個の点を除いただけであるから.)
を,
の正則値から,その逆像である正則点の個数を与える関数とすると,これは有限の値を取る局所定数関数になる.
しかし,先に示した補題から, は正則値全体で定数関数になる.
さらに,任意の の正則値
で
であることも分かる.もし,ある正則値
で
であるとき,
が定数関数であることから,任意の正則値で
となるが,このとき
の像はすべて臨界値となり,
全体が臨界点となるが,臨界点が有限個であったことに矛盾する.
よって,定数関数 は
でない.さらに,臨界値は臨界点から来るので,
の値域である
の点は正則値であっても臨界値であっても
によってその点に対応するような
の点が存在するので,
は全射である.
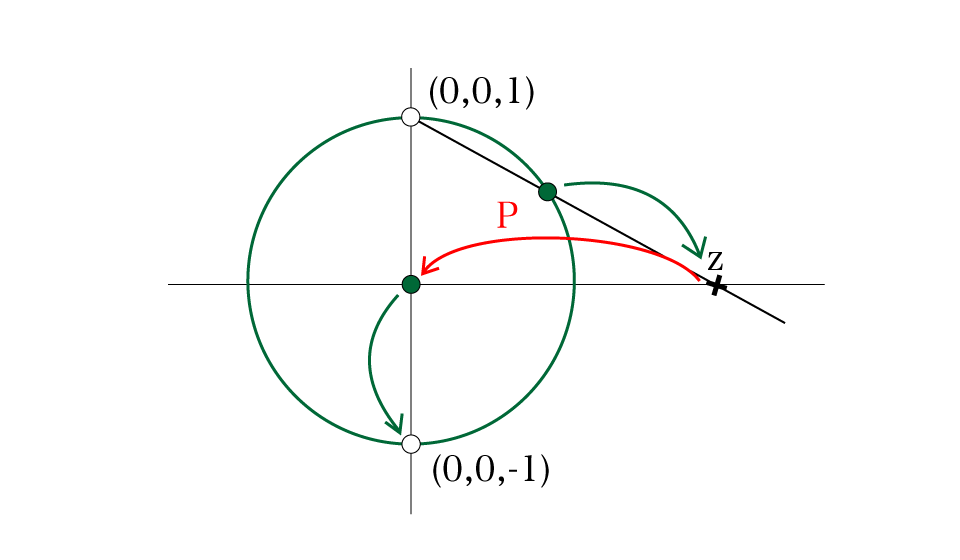
よって, で送ると南極に行くような点が少なくとも1つ存在する.その点は道中で
によって
に送られているので,
は必ず1つ零点をもつ.
以上です.だいたいこんな感じです.ありがとうございました.
Hartshorne §1 Varieties, Lemma 4.3
見切れている数式はスクロールで表示できます.
本記事における多様体は代数多様体のうちアフィン多様体,準アフィン多様体,射影多様体,準射影多様体のいずれかのことを言い,多様体がアフィンであるとは何らかのアフィン多様体と同型であることを言う.
命題
命題だけ言われてもなんのこっちゃですが,これを示します.
証明
テキストでは次のステートメントを証明します:
これは, を固定して
の任意の点
に対してそのような開集合
が存在すると,
の中で
を動かしてもそれに応じて
の中に開集合が取れます.このようにして得られる開集合たちは
を覆い尽くすので,
を生成していると言えます.これが任意の開集合についても言える(任意の開集合がアフィン開集合で覆える)ので,元の命題が示されたと言えます.
ということで改付きの命題を示すわけですが,加えてこの命題にさらなる単純化を与えます.
まずはじめに,命題の中で の開近傍
を取っていますが,
自体も(多様体の開集合,つまり一般的に言えば準射影多様体であるという意味で)多様体であるので,そもそも多様体全体を取って来て
としても良いことが言えます.
さらに,多様体は(一般的に言えば準射影多様体であるという意味で)準アフィン多様体と同型な開被覆が存在する()ので,
自体も
における準アフィン多様体と同型であるとして良いことが言えます.
よって,結局以下のステートメントを証明すれば良いことがわかります:
さて, は準アフィン多様体ということで,何らかのアフィン多様体の開集合となっているので,閉集合
について
と表せることが定義から言えます.さらに, であり,
が
を含む最小の閉集合であることから
となるので,
であることがわかりますが,一方で であり,書き直すと
となりますが,
\begin{align*} \overline{Y} - Z_2 &\supseteq Z_1 - Z_2 - Z_2\\ &= Z_1 - Z_2\\ &= Y \end{align*}
ということで ということが言え,
従って
が成り立ちます.
ここで, が
の閉集合であるので,
とします.すると,
と変形できます.しかし,それぞれの について,
であることから
\begin{align*} Y - V(f_i) &\supseteq \overline{Y} - V(f_i) - V(f_i)\\ &= \overline{Y} - V(f_i)\\ &\supseteq Y - V(f_i) \qquad (\because \overline{Y} \supseteq Y) \end{align*}
となります.よって
となるので,
と表すことができます.
ここで, は
の中の閉集合であり,さらに
も
の中で閉集合なので,
は
の開集合となります.よって任意の点
は,あるアフィン開集合
に含まれるので,命題がなりたちます.
考察
教科書とは少し違った証明をしてみました.では,これはどのような時に使えるのか,ということを考えてみたいと思います.
いま2次元のアフィン平面 にいるとします.
「あ〜原点をとりのぞきて〜」
と思うことってよくあると思います.
ありますねぇ!!
よし!(迫真)
というわけで,平面から原点を取り除いたものを とします.

ちょっと見切れてしまいましたが,真ん中の点が原点で,それを取り除くので は開集合です.本文では
という数式が出てきましたが,今の場合 は平面全体の
ですが,例えば原点を通るような直線の多項式として
と
とすると,

図では左が ,右が
ですが,それぞれ閉包である全体から直線を取り除いたものですが,それらの和集合をとると考えたい
になっています.
本文での言及から,これらが のアフィン開集合であることも同様に言えます.

このようにして,一般の(準射影多様体であるという意味での)多様体についても,その閉包からある閉集合を除いたものの和集合で表すことができ,実はそれぞれがアフィンだということが言える,というのがこの命題の言わんとしていることだと思います.
以上です.ありがとうございました.
段論 #1 導入・簡単な例

見切れている数式はスクロールで見れます
本記事は,上の記事を受けて理論をより単純な形で一般化することを目的とし,前記事では触れられなかった他の例について考察を与えるものである.この記事には前記事の訂正や改良を含み,主要な動機については省略する.
定義
前記事では としたが,
としても掛け算について
を単位元に持つモノイドをなすという条件を満たすので,本記事においては後者を採用する.さらに,環は単位元を持つとする.
さて,前記事では単位元 をもつモノイド
について,その自由群に同値関係を入れて環を構成したが,これは冗長だった.初めから直接環を作りに行く.まず,
を単なる文字の集合とみなし,その形式的な逆文字集合を
とする.これはつまり,
に対して
とする,ということである. を文字集合とし,
を
の文字からなる語全体の集合とすると,語
について
と演算を定義すると,空語 を単位元に持つモノイドをなす.
ここまでは前記事と同じである.次に,モノイド準同型 について,語の簡約化を
- 語
をなす文字
について,
ならば
を
に,
ならば
を
に変換する.
と
が隣り合う部分を空語に変換する.
とし,語 について簡約化を
と表す.
上の同値関係を
と定義する.この同値関係で割ることによって を得る.
証明 示すべきことは4つある.
ここで, がモノイドであることから,明らかに2までは成り立つ.また任意の
について,
であるとき,
とすると,
となり,逆元が存在する.さらに, より,簡約化の構成から交換法則を満たす.以上より成り立つ.
次に, に
の演算を誘導する.
の逆文字
と
について,
とし,同様に
とし,それぞれの逆文字については
と定義する.これを用いて一般の語の積を,,
について
とし,特に空語 については
と定義する.すると, について
となり,一般の についても
\begin{align*} \mathbf{x} \cdot e &= (x_1 \cdot e, \ldots, x_r \cdot e)\\ &= (x_1, \ldots, x_r)\\ &= \mathbf{x} \end{align*}
\begin{align*} e \cdot \mathbf{x} &= (e \cdot x_1, \ldots, e \cdot x_r)\\ &= (x_1, \ldots, x_r)\\ &= \mathbf{x} \end{align*}
となるので, は
においても演算
の単位元になる.
証明 について,それぞれ
,
,
とすると
\begin{align*} (\mathbf{x} + \mathbf{y}) \cdot \mathbf{z} &= (x_1, \ldots, x_r, y_1, \ldots, y_s) \cdot (z_1, \ldots, z_t) \\ &= (x_1 \cdot z_1, x_1 \cdot z_2, \ldots, x_r \cdot z_t, y_1 \cdot z_1, \ldots, y_s \cdot z_t)\\ &= (x_1 \cdot z_1, x_1 \cdot z_2, \ldots, x_r \cdot z_t) + (y_1 \cdot z_1, \ldots, y_s \cdot z_t)\\ &= \mathbf{x} \cdot \mathbf{z} + \mathbf{y} \cdot \mathbf{z} \end{align*}
となり,さらに
\begin{align*} \mathbf{x} \cdot (\mathbf{y} + \mathbf{z}) &= (x_1, \ldots, x_r) \cdot (y_1, \ldots, y_s, z_1, \ldots, z_t) \\ &= (x_1 \cdot y_1, x_1 \cdot y_2, \ldots, x_1 \cdot y_s, x_1 \cdot z_1, \ldots, x_1 \cdot z_t, \ldots, x_r \cdot z_t) \\ \end{align*}
となるが,演算 の可換性から適宜文字を入れ替えて
\begin{align*} &= (x_1 \cdot y_1, x_1 \cdot y_2, \ldots, x_1 \cdot y_s, x_1 \cdot z_1, \ldots, x_1 \cdot z_t, \ldots, x_r \cdot z_t) \\ &= (x_1 \cdot y_1, x_1 \cdot y_2, \ldots, x_r \cdot y_s, x_1 \cdot z_1, \ldots, x_r \cdot z_t) \\ &= \mathbf{x} \cdot \mathbf{y} + \mathbf{x} \cdot \mathbf{z} \end{align*}
となり,分配法則を満たす.以上より成り立つ.
性質
証明 について,
は
(ただし ,
) となる.
の部分については
であり, の部分については
となる.よって全体としては
となるので,簡約化すると補題の式を得る.
証明 補題1.4より任意の でない
は
の単位元
もしくはその形式的逆元
の和で表せる.
と
を定義し,
を
と定義すると,これは環準同型になる.また明らかに であり,任意の
について
あるいは
と一意に表せるので,
あるいは
を
で引き戻して
となる
を得る.よって
は全単射となる.
証明 () 明らか.
()
の可換性は
に誘導される.これは
と
について
であることから成り立つ.よって,任意の についても
\begin{align*} \mathbf{x} \cdot \mathbf{y} &= (x_1, \ldots, x_r) \cdot (y_1, \ldots, y_s)\\ &=(x_1 \cdot y_1, x_1 \cdot y_2, \ldots, x_r \cdot y_s)\\ &=(y_1 \cdot x_1, y_2 \cdot x_1, \ldots, y_s \cdot x_r)\\ &=(y_1 \cdot x_1, y_1 \cdot x_2, \ldots, y_s \cdot x_r)\\ &= \mathbf{y} \cdot \mathbf{x} \end{align*}
となり可換となる.
証明 を
と定義すると,
について
\begin{align*} &f(x^{-1} \cdot_S y) \\ &= f( (x \cdot_S y)^{-1} )\\ &= (f(x \cdot_S y))^{-1} \\ &= (f(x) \cdot_T f(y))^{-1}\\ &= (f(x))^{-1} \cdot_T f(y)\\ &= f( x^{-1} ) \cdot_T f(y) \end{align*}
より,
となるので,モノイド準同型となる.
証明 はモノイド準同型より,これを梯とする下段環を自然に構成できる.
以下, について
と表す.
証明 について
と定義する.このとき, であり,
について
\begin{align*} &L_N(f)(\mathbf{x} + \mathbf{y}) \\ =& L_N(f) ( (x_1, \ldots, x_r, y_1, \ldots, y_s) ) \\ =&( f(x_1), \ldots, f(x_r), f(y_1), \ldots, f(y_s) ) \\ =&( f(x_1), \ldots, f(x_r) ) + ( f(y_1), \ldots, f(y_s) ) \\ =&L_N(f)(\mathbf{x}) + L_N(f)(\mathbf{y}) \end{align*}
\begin{align*} &L_N(f)(\mathbf{x} \cdot_{L_N(S)}\mathbf{y}) \\ =& L_N(f)( (x_1 y_1, x_1 y_2, \ldots, x_r y_s) ) \\ =&( f(x_1 y_1), f(x_1 y_2), \ldots, f(x_r y_s) ) \\ =&( f(x_1) f(y_1), f(x_1) f(y_2), \ldots, f(x_r) f(y_s) ) \\ =&( f(x_1), \ldots, f(x_r) ) \cdot_{L_N(T)} ( f(y_1), \ldots, f(y_s) ) \\ =&L_N(f)(\mathbf{x}) \cdot_{L_N(T)} L_N(f)(\mathbf{y}) \end{align*}
となり,環準同型となる.
今回は以上です.査読お願い致します.
モノイド上の自由群の剰余群の代数構造と準加算について

見切れている数式はスライドで表示できます.
この記事では は0を含まないとし、通常の積について単位元1をもつモノイドだと考える.この記事はまずはじめに形式的な議論を述べ,次に例と考察を与える.
本論
を単位元
をもつモノイドとし,その演算を
とする.
の自由群を
とし,その群としての演算を便宜上
と表す.ここで,
上の同値関係を以下のように定義する.まず,
をモノイド準同型,
を
- 語
をなす文字
について,
ならば
を
に,
ならば
を
に変換する.
と
が隣り合う部分を空語に変換する.
というステップを経て語を与える写像とする.これを用いて同値関係を
と定義し、 とする.さらに,
の演算を
に誘導する.
の逆文字
と
について,
とし,同様に
とし,それぞれの逆文字については
と定義する.これを用いて一般の語の積を,,
について
とし,特に空語 については
と定義する.
証明 まず,構成より は演算
について単位元
を持つアーベル群をなす.さらに,上述の定義から演算
について単位元
を持つモノイドをなす.さらに,
について,それぞれ
,
,
とすると
\begin{align*} (\mathbf{x} + \mathbf{y}) \cdot \mathbf{z} &= (x_1, \ldots, x_r, y_1, \ldots, y_s) \cdot (z_1, \ldots, z_t) \\ &= (x_1 \cdot z_1, x_1 \cdot z_2, \ldots, x_r \cdot z_t, y_1 \cdot z_1, \ldots, y_s \cdot z_t)\\ &= (x_1 \cdot z_1, x_1 \cdot z_2, \ldots, x_r \cdot z_t) + (y_1 \cdot z_1, \ldots, y_s \cdot z_t)\\ &= \mathbf{x} \cdot \mathbf{z} + \mathbf{y} \cdot \mathbf{z} \end{align*}
となり,さらに
\begin{align*} \mathbf{x} \cdot (\mathbf{y} + \mathbf{z}) &= (x_1, \ldots, x_r) \cdot (y_1, \ldots, y_s, z_1, \ldots, z_t) \\ &= (x_1 \cdot y_1, x_1 \cdot y_2, \ldots, x_1 \cdot y_s, x_1 \cdot z_1, \ldots, x_1 \cdot z_t, \ldots, x_r \cdot z_t) \\ \end{align*}
となるが,演算 の可換性から適宜文字を入れ替えて
\begin{align*} &= (x_1 \cdot y_1, x_1 \cdot y_2, \ldots, x_1 \cdot y_s, x_1 \cdot z_1, \ldots, x_1 \cdot z_t, \ldots, x_r \cdot z_t) \\ &= (x_1 \cdot y_1, x_1 \cdot y_2, \ldots, x_r \cdot y_s, x_1 \cdot z_1, \ldots, x_r \cdot z_t) \\ &= \mathbf{x} \cdot \mathbf{y} + \mathbf{x} \cdot \mathbf{z} \end{align*}
となり,分配法則を満たす.以上より成り立つ.
具体例
自然数から整数へ
を
以上の整数全体とすると,これは通常の掛け算について単位元
を持つモノイドをなす.
上の自由群を以下のように構成する.まず
をただの文字の集合だと思い,
を逆文字全体の集合,つまり
とする. とし,
を 文字集合
の文字からなる有限長の文字列(これを語という)全体の集合とすると,
という演算 について空語
を単位元とするモノイドをなす.語
について,語に含まれる文字
と逆文字
が連続して現れる部分を空語に置き換えたものを簡約化
とし,
上の同値関係を
と定義し, とすると,
は群になり,これが自由群である.さらに,
を
と定義すると,これはモノイド準同型となり,これを用いて
を上述のように構成する.例えば,
という語については
\begin{align*} (2,3^{-1}) &\mapsto (1,1,1^{-1},1^{-1},1^{-1})\\ &\mapsto (1,1^{-1},1^{-1})\\ &\mapsto (1^{-1}) \end{align*}
となるので簡約化は となる.これを用いて自由群上の同値関係を
と定義し, とする.ここにモノイド
の演算を上述のように誘導する.このようにして下のレベルの演算を持つ環
を得るが,なんのことはなくこれはただの整数環
である.これは空語
を通常の
,逆文字
を 通常の和の逆元
と思えば直ちに分かる.実際,
の中では
であったが,これは単に
という式を形式的な元として表しているだけである.
このように,下のレベルの演算を得る際には,元の集合にはなかった単位元と逆元を添加し,和を式ではなく自由群の元として見ることが重要である.
整数から下整数へ
では,整数より下のレベルを実際に構成してみる.まず, を
以上の整数全体の集合とすると,通常の和
について
を単位元とするモノイドをなす.先ほどと同様に自由群を構成し,これを
をする.ここで,
を
とすると,
\begin{align*} &N(n+m) = 2^{n+m} = 2^n \cdot 2^m = N(n) \cdot N(m)\\ &N(0) = 2^{0} = 1 \end{align*}
となり,これはモノイド準同型になる.これを使って同様に を構成する.この環の和をしきたりに倣って
とすると,例えば
\begin{align*} 1 \oplus 1 &= (1,1)\\ &\sim (0,0,0,0) \qquad (2^1 = 2)\\ &\sim 2 \qquad (2^2 = 4) \end{align*}
みたいになる.しかし,
\begin{align*} 2 \oplus 1 &=(2,1)\\ &\sim (0,0,0,0,0,0) \end{align*}
となるが,これに対応する整数は存在しない.
まとめ
以上のように,任意のモノイドについてその演算と分配法則を満たすようなの下のレベルの演算を併せ持つ環を構成した.これはもちろん準加算の発想が元となってはいるが,最もプレーンな発想からは少し遠ざかっている.これは「いくつか繰り返すと和を得るような演算」というよりは,「元々の演算と分配法則を満たすような演算によって環を構成する」ことを動機としたことによる.構成の始まりを群からにすると具体的にどのような変化があるのかを次回以降のテーマとする.
Hartshorne Ex2.14 The Segre Embedding #1
見切れている数式はスライドで表示できます.
久しぶりに本題に戻って抜本の演習をやりますねぇ!
特にこれは自分の学部卒業論文でも取り扱ったものなので個人的に思い入れのある演習問題です.がんばって解説します.
セグレ埋め込みとは,2つの射影空間からそれらの積への埋め込みであるような写像のひとつです.
セグレ埋め込みの構成法の動画です.
— だふやふ (@dafuyafu) 2018年4月3日
(ブログ用) pic.twitter.com/689g29hUj8
具体的には上の動画のように,行列の積のようにして射影空間の点の斉次座標を掛け合わせた点へ送る写像のことです.以下,この記事では の点を
\begin{equation} P = \begin{array}{rcccl} \bigl[& z_{00}:&\cdots& :z_{0n}: &\ \\ &\vdots& \ddots& \vdots&\\ &: z_{m0}:& \cdots& :z_{mn} &\bigr] \end{array} \end{equation}
のように添え字を付けて表します.
まず,やることとして,
をそれぞれ見ていきたいと思います.
 が well-defined であること
が well-defined であること
は同値類(ここでは射影空間の点の斉次座標)の表示によっているので,写像として well-defined であることを示さなければなりません.
と
が
と,0でない と
を用いて表されるとき,右側の表示である
と
を用いて
を
で送ると,
\begin{align*} \psi (P',Q') &= \psi (\left[ \lambda x_0:\cdots: \lambda x_m \right] \times \left[ \omega y_0:\cdots: \omega y_n \right])\\ &= \left[ \lambda x_0 \cdot \omega y_0: \cdots : \lambda x_m \cdot \omega y_n \right]\\ &= \left[ (\lambda \omega) x_0 y_0 : \cdots : (\lambda \omega) x_m y_n \right]\\ &\sim \left[ x_0 y_0 : \cdots : x_m y_n \right] \qquad (\because \lambda \omega \neq 0)\\ &= \psi (\left[ x_0:\cdots:x_m \right] \times \left[ y_0:\cdots:y_n \right])\\ &= \psi (P,Q) \end{align*}
となるので,斉次座標のとり方によらず,well-defined である.
 が単射であること
が単射であること
埋め込みという名の通り, が単射であることを示します.
と
が
と表されているとき,それぞれ射影空間の点であるので, についてはある
(ただし
)が存在して
,
についてもある
(ただし
)が存在して
が成り立つ.ここで,それぞれ
としても一般性を失わない.
このとき, をそれぞれ
\begin{align*} P &= \left[ x_0 : x_1 : \cdots: x_m \right]\\ &\sim \left[ 1 : x_1 / x_0 : \cdots : x_m / x_0 \right]\\ &= \left[ 1 : p_1 : \cdots : p_m \right]\\ \\ Q &= \left[ y_0 : y_1 : \cdots: y_n \right]\\ &\sim \left[ 1 : y_1 / y_0 : \cdots : y_n / y_0 \right]\\ &= \left[ 1 : q_1 : \cdots : q_n \right] \end{align*}
と表す.この点 を
で送ると,
\begin{equation*} \psi (P,Q) = \begin{array}{rccccl} \bigl[& 1:& q_1 :& \cdots & q_n: &\\ &p_1:& p_1 q_1 :& \cdots & \vdots& \\ &\vdots & \vdots & \ddots & \vdots& \\ &p_m:& \cdots& &: p_m q_n &\bigr] \end{array} \qquad(1) \end{equation*}
となる.ここで,同様に を
とする.ここで, であるとき
となるが,この点を
で送ると,
\begin{equation*} \psi (P',Q') = \begin{array}{rccccl} \bigl[& 0:& 0 :& \cdots & 0: &\\ & x_1 y_0:& x_1 y_1 :& \cdots & \vdots& \\ &\vdots & \vdots & \ddots & \vdots& \\ & x_m y_0:& \cdots& &: x_m y_n &\bigr] \end{array} \qquad (2) \end{equation*}
となり, の座標を(1)と比較すると
となる.
のときも同様である.さらに,
かつ
のとき,
と同様に
\begin{align*} P' &= \left[ x'_0 : x'_1 : \cdots: x'_m \right]\\ &\sim \left[ 1 : x'_1 / x'_0 : \cdots : x'_m / x'_0 \right]\\ &= \left[ 1 : p'_1 : \cdots : p'_m \right]\\ \\ Q' &= \left[ y'_0 : y'_1 : \cdots: y'_n \right]\\ &\sim \left[ 1 : y'_1 / y'_0 : \cdots : y'_n / y'_0 \right]\\ &= \left[ 1 : q'_1 : \cdots : q'_n \right] \end{align*}
と表す.この点 を
で送ると,
\begin{equation*} \psi (P',Q') = \begin{array}{rccccl} \bigl[& 1:& q'_1 :& \cdots & q'_n: &\\ &p'_1:& p'_1 q'_1 :& \cdots & \vdots& \\ &\vdots & \vdots & \ddots & \vdots& \\ & p'_n:& \cdots& &: p'_m q'_n &\bigr] \end{array} \qquad (3) \end{equation*}
となる.ここで, とすると(1)と(3)において,最も上の行,最も左の列を比較すると
であることが分かる.1
よって ,
となり,
となる.よって
は単射となる.
準備が大変なので残りは次回に回します.
-
一般に射影空間の点
(ただし
)が点として等しいとき,ある
が存在して
となるが,今の場合それぞれの点の
の座標が
となり数として等しいので
である.以上のことから単純に座標を比較している.↩