Milnor - The Fundamental Theorem of Algebra (Topology from the Differentiable Viewpoint)
見切れている数式はスクロールで読めます.
今日は趣向を変えてミルナー著「Topology from the Differentiable Viewpoint」から代数学の基本定理の証明を紹介します.ちょうど微分トポロジーの授業でここの部分が僕の担当だったからです.
代数学の基本定理は複素数体が代数閉体であるというものですが,なんか沢山証明方法はあるみたいですが,ミルナー本にあるやつを解説したサイトは見かけなかったので,今日はそこを書いてみるなー(激ウマギャグ)
流れ
まず証明の流れから説明すると,
- 一変数複素係数多項式とステレオグラフ射影を用いて単位球面から単位球面への写像を考える.
- その写像が単位球面上滑らかであることを示す.
- さらにその写像が全射であることを,正則点の個数の関数を用いて示す.
- 定理に結びつける.
という感じです.
証明
(証明)
任意の について,
(ただし
) を用いて
と表されているとする. は
から
への関数を定めるが,実部と虚部に分けて考えても2つとも多項式で表されているので,通常の微分に関して滑らかである.
今、3次元実ユークリッド空間 に単位球面
があると考える.

ここで,単位球面の北極 から
平面へのステレオグラフ射影
を考える.
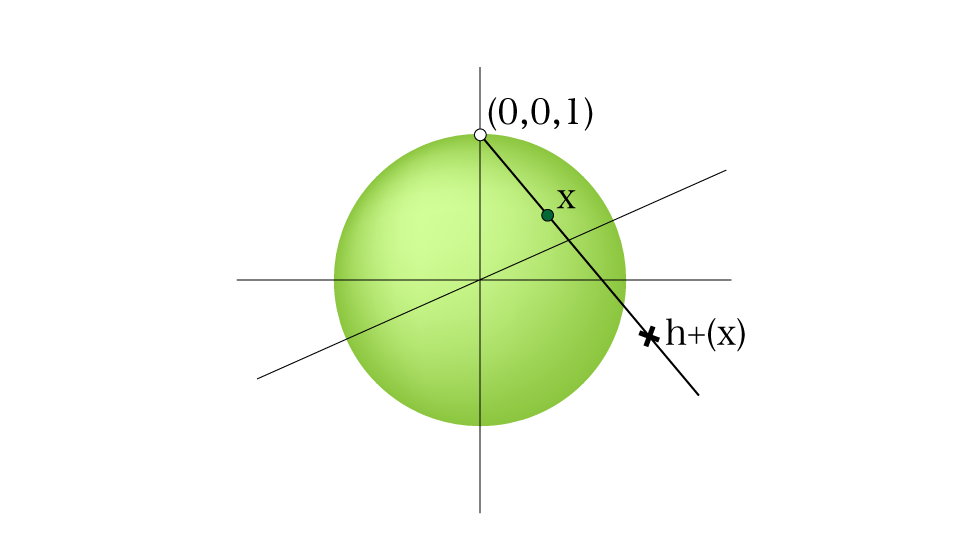
定式的には,
となり,北極以外の の点
を,北極から
に引いた半直線が
平面にぶつかる点に送る滑らかな写像である.
これらを用いて次のような写像 を考える.
\begin{equation} f(x) = \begin{cases} h_+^{-1} \circ P \circ h_+ (x) & (x \neq (0,0,1))\\ (0,0,1) & (x = (0,0,1)) \end{cases} \end{equation}
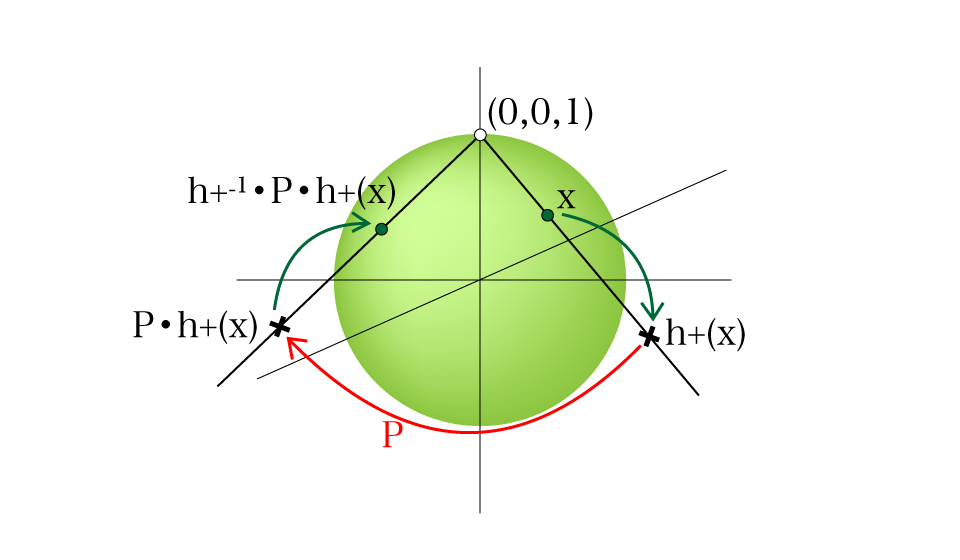
これは,単位球面上の 以外の点を
平面上にステレオグラフ射影し,この平面を複素平面だと思って
で別の複素数に送り,ステレオグラフ射影で単位球面に引き戻すような写像である.
 が
が  上滑らかであること
上滑らかであること
構成より, は
においては滑らかな写像の合成であるので,
もまた滑らかである.これが
の近傍においても,つまり定義域において
が滑らかな写像であることを示す.まず,南極
から
平面へのステレオグラフ射影を
とし,
を
とする.
においては,
であることから,
と表される.ここで, を計算する.

複素数 を含むように空間を縦で割ると上図のように表される.

赤色と青色の三角形は「直角以外の一つの角が等しい」ので相似である.
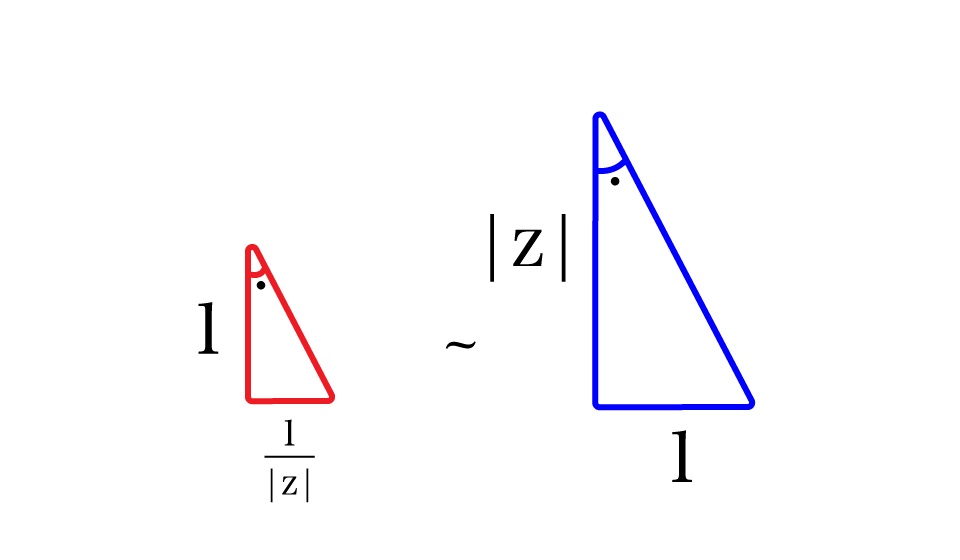
すると,赤色の三角形のうち,ちょうど のノルムに対応する辺の長さは
であることが分かる.よって,求めたい実際の複素数
は,その単位ベクトルにノルムをかけたものであるので,
\begin{equation} h_+ \circ h_-^{-1}(z) = \frac{1}{|z|} \cdot \frac{z}{|z|} = \frac{1}{\overline{z}} \end{equation}
以上のことから, を整理する.複素共役は積や和に分解し,複素共役の複素共役は元の複素数になることなどを用いると,
\begin{align*} Q(z) &= h_- \circ h_+^{-1} \circ P \circ h_+\circ h_-^{-1} (z)\\ &= h_- \circ h_+^{-1} \circ P (1/\overline{z})\\ &= h_- \circ h_+^{-1} (a_0 (1/\overline{z})^n + \cdots + a_{n-1} (1/\overline{z}) + a_n)\\ &= 1 / \overline{(a_0 (1/\overline{z})^n + \cdots + a_{n-1} (1/\overline{z}) + a_n)}\\ &= 1 / (\overline{a_0} \overline{(1/\overline{z})^n} + \cdots + \overline{a_{n-1}} \overline{(1/\overline{z})} + \overline{a_n})\\ &= 1 / (\overline{a_0} (1/z)^n + \cdots + \overline{a_{n-1}} (1/z) + \overline{a_n})\\ &= z^n / (\overline{a_0} + \overline{a_1} z + \cdots + \overline{a_n} z^n) \end{align*}
となる.すると, であることから
は
においても値
をもち,さらに有理関数の形で表されるので滑らかな関数である.よって,
もまた滑らかな関数となる.
 の臨界値が高々有限個であること
の臨界値が高々有限個であること
は複素関数であり,実部と虚部に分けることで実数値関数の対と考えることができる.つまり,実数係数多項式
を用いて
と表すことができる.ここで,
は多項式によって表される関数であるので複素正則関数である.よってコーシー・リーマンの方程式が成り立つ.今の場合,
\begin{equation} \frac{\partial P_1}{\partial x} = \frac{\partial P_2}{\partial y},\quad \frac{\partial P_1}{\partial y} = - \frac{\partial P_2}{\partial x} \end{equation}
となる.また,
\begin{equation} \frac{d P_1}{d x} = \frac{\partial P_1}{\partial x} + \sqrt{-1} \frac{\partial P_2}{\partial x} \end{equation}
となる.
これを複素数だと思うと,そのノルムの二乗は
\begin{equation} \begin{array}{|c|} \frac{d P_1}{d x} \end{array}^2 = \left( \frac{\partial P_1}{\partial x} \right)^2 + \left( \frac{\partial P_2}{\partial x} \right)^2 \end{equation}
となるが,複素関数 のヤコビ行列
は
\begin{equation} J(P) = \left[ \begin{array}{cc} \frac{\partial P_1}{\partial x} & \frac{\partial P_1}{\partial y}\\ \frac{\partial P_2}{\partial x} & \frac{\partial P_2}{\partial y} \end{array} \right] \end{equation}
となることから,ヤコビ行列の行列式は
\begin{equation} \mathrm{det} J(P)= \left( \frac{\partial P_1}{\partial x} \right)^2 + \left( \frac{\partial P_2}{\partial x} \right)^2 \end{equation}
となり,ちょうど
\begin{equation} \begin{array}{|c|} \frac{d P_1}{d x} \end{array}^2 = \mathrm{det} J(P) \end{equation}
となることが分かる.ここで,ヤコビ行列の行列式が になる点が
の臨界点であることから,
の臨界点は
である点に対応することが分かる.しかし,
は定数でない多項式であったので,
もまた多項式であるので,
になる点は有限個しかない.
よって の臨界点は有限個しかないので,構成から
もまた臨界点は有限個しかなく,故に臨界値は有限個に限られる.
連結位相空間上の局所定数関数は定数関数であること
ここで,題にあるような補題を証明する.
を連結空間,
を局所定数関数とする.任意の
の点
を一つ固定して考える.
を
とする.定義から,,
である.
ここで, がそれぞれ
の開集合であることを示す.
任意に を取る.定義より
である.ここで,
は定数関数であることから,ある
を含む開集合
が存在して,任意の
について
となる.
よって,任意の について
となるので
となる.
ここで,任意に取った を
の中で動かすことで,
は
を被覆することが分かる.つまり,
\begin{equation} C_0 = \bigcup_{y_i \in C_0} U_i \end{equation}
となる.各 は開集合なので,その可算個の和集合である
もまた開集合となる.同様にして
も開集合であることが示せる.
以上より は開集合となるが,
は連結空間なので,交わらない開集合で分割することはできないはずである.よって
のいずれかになる.しかし,今 を固定して考えていたが,
自体は
を満たすので,
であることから,
は空集合ではない.よって1つめのパターンとなる.
よって 全体で
は一定の値を取るので,全体でも定数関数となる.
帰結
今, は連結空間である.
の臨界値は有限個であったので,正則値全体は連結である.(
無限連結空間から有限個の点を除いただけであるから.)
を,
の正則値から,その逆像である正則点の個数を与える関数とすると,これは有限の値を取る局所定数関数になる.
しかし,先に示した補題から, は正則値全体で定数関数になる.
さらに,任意の の正則値
で
であることも分かる.もし,ある正則値
で
であるとき,
が定数関数であることから,任意の正則値で
となるが,このとき
の像はすべて臨界値となり,
全体が臨界点となるが,臨界点が有限個であったことに矛盾する.
よって,定数関数 は
でない.さらに,臨界値は臨界点から来るので,
の値域である
の点は正則値であっても臨界値であっても
によってその点に対応するような
の点が存在するので,
は全射である.
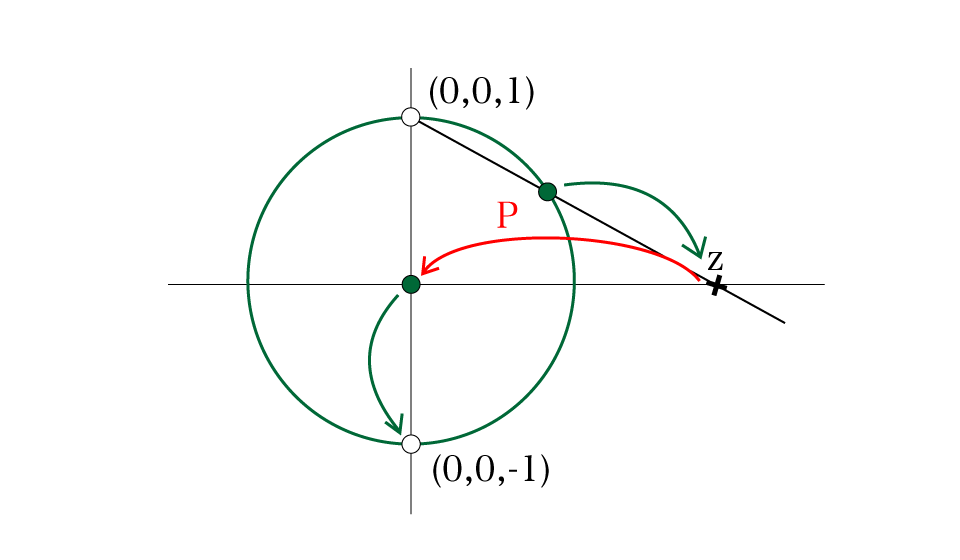
よって, で送ると南極に行くような点が少なくとも1つ存在する.その点は道中で
によって
に送られているので,
は必ず1つ零点をもつ.
以上です.だいたいこんな感じです.ありがとうございました.